Belajar Memprogram Komputer Kuantum (1): Dasar Komputasi Kuantum dan Cara Menginstal Qiskit
Komputer kuantum, seperti yang telah dijelaskan di artikel sebelumnya, adalah mesin penghitung yang memanfaatkan perilaku "aneh" dari benda-benda berukuran kecil. IBM, salah satu perusahaan yang mengembangkan komputer kuantum, mengembangkan sebuah perangkat lunak sumber terbuka (open source software) yang dapat digunakan untuk memprogram komputer kuantum.
Perangkat lunak ini bernama quantum information science kit (Qiskit). Qiskit memungkinkan kita untuk membuat program, menyimulasikan, bahkan menjalankan program langsung di komputer kuantum sebenarnya milik IBM, IBM Q, dari komputer pribadi kita. Dalam seri tutorial ini kita akan belajar dasar-dasar membuat program komputasi kuantum dengan Qiskit.
Untuk dapat mengikuti tutorial ini yang anda butuhkan adalah pengetahuan tentang aljabar linier, operasi hitung matriks dan vektor, yang sudah dipelajari di bangku SMA. Selain itu, dibutuhkan juga pengetahuan tentang pemrograman (utamanya dengan python) di tingkat dasar. Tentunya, karena kita akan mempelajari bagaimana memprogram komputer kuantum, kita membutuhkan sedikit pengetahuan tentang sains informasi kuantum.
Untuk tutorial kali ini, kita akan mulai dengan belajar tentang dasar-dasar sains informasi kuantum yang dibutuhkan dalam pemrograman kuantum komputer di tutorial yang akan datang. Selanjutnya, kita akan belajar bagaimana menginstal Qiskit di komputer pribadi kita masing-masing.
Dasar komputasi kuantum
Sebelum memulai pemrograman komputer kuantum, kita butuh untuk belajar tentang dasar-dasar sains informasi kuantum. Kita akan mempelajari bagaimana merepresentasikan bit kuantum dan gerbang-gerbang logika dasar dalam pemrosesan informasi kuantum.
Qubit
Satuan terkecil informasi kuantum disebut qubit (dibaca: kiubit), kependekan dari quantum bit, yang direpresentasikan dalam notasi matematika  dan
dan  . Simbol
. Simbol 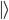 di kiri dan kanan angka
di kiri dan kanan angka  dan
dan  disebut ket. Sebuah ket tidak lain hanyalah representasi sebuah vektor. Qubit
disebut ket. Sebuah ket tidak lain hanyalah representasi sebuah vektor. Qubit  dan
dan  direpresentasikan dalam vektor berikut:
direpresentasikan dalam vektor berikut:
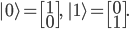
Bola Bloch
Seperti yang dijelaskan sebelumnya, sebuah qubit direpresentasikan sebagai sebuah vektor. Penggambaran mudah bagi qubit adalah dengan menggunakan sebuah bola, satu vektor qubit dapat mengarah pada sembarang permukaan bola (Gambar 1). Perhatikan Gambar 1, qubit  mengarah vertikal ke atas sejajar sumbu-
mengarah vertikal ke atas sejajar sumbu- positif (Gambar 1A) dan qubit
positif (Gambar 1A) dan qubit  mengarah vertikal ke bawah sejajar sumbu-
mengarah vertikal ke bawah sejajar sumbu- negatif (Gambar 1B). Selain
negatif (Gambar 1B). Selain  dan
dan  , qubit dapat mengarah ke permukaan mana pun di permukaan bola di antara dua ekstrem
, qubit dapat mengarah ke permukaan mana pun di permukaan bola di antara dua ekstrem  dan
dan  . Keadaan ini disebut superposisi, direpresentasikan sebagai kombinasi linier dari
. Keadaan ini disebut superposisi, direpresentasikan sebagai kombinasi linier dari  dan
dan  (Gambar 1C):
(Gambar 1C):

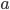 dan
dan  merupakan bilangan kompleks yang masing-masing merupakan probabilitas ditemukannya qubit
merupakan bilangan kompleks yang masing-masing merupakan probabilitas ditemukannya qubit  dan
dan  . Keadaan ini juga dapat direpresentasikan dengan parameter-parameter dalam koordinat bola (Gambar 1C) untuk menunjukkan posisi vektor dalam bola Bloch:
. Keadaan ini juga dapat direpresentasikan dengan parameter-parameter dalam koordinat bola (Gambar 1C) untuk menunjukkan posisi vektor dalam bola Bloch:

Dengan  dan
dan  masing-masing adalah sudut polar dan sudut azimut dalam sistem koordinat bola.
masing-masing adalah sudut polar dan sudut azimut dalam sistem koordinat bola.

Gambar 1. Bola Bloch untuk menggambarkan keadaan qubit  (A), keadaan qubit
(A), keadaan qubit  (B), dan keadaan superposisi antara
(B), dan keadaan superposisi antara  dan
dan  (C); perhatikan posisi dan arah panah merah pada tiap keadaan; panah pada keadaan C merupakan salah satu posisi dari probabilitas yang ada.
(C); perhatikan posisi dan arah panah merah pada tiap keadaan; panah pada keadaan C merupakan salah satu posisi dari probabilitas yang ada.
Gerbang Pauli-X
Gerbang logika ini bekerja layaknya gerbang logika NOT dalam gerbang logika klasik; mengubah logika  menjadi
menjadi  dan sebaliknya. Gerbang Pauli-X mengubah qubit
dan sebaliknya. Gerbang Pauli-X mengubah qubit  menjadi
menjadi  begitu pula sebaliknya. Gerbang Pauli-X direpresentasikan sebagai matriks
begitu pula sebaliknya. Gerbang Pauli-X direpresentasikan sebagai matriks

Sehingga, jika kita lakukan operasi gerbang Pauli-X terhadap qubit akan didapatkan:

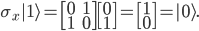
Gambar 2B menujukkan operasi gerbang Pauli-X dalam bola Bloch. Vektor qubit  dirotasikan 180
dirotasikan 180 terhadap sumbu-
terhadap sumbu- . Selain gerbang Pauli-X terdapat pula gerbang Pauli-Y dan gerbang Pauli-Z yang pada intinya adalah merotasikan vektor dalam bola Bloch sebesar 180
. Selain gerbang Pauli-X terdapat pula gerbang Pauli-Y dan gerbang Pauli-Z yang pada intinya adalah merotasikan vektor dalam bola Bloch sebesar 180 terhadap masing-masing sumbu-
terhadap masing-masing sumbu-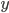 dan sumbu-
dan sumbu-

Gambar 2. Keadaan kuantum awal  (A), keadaan kuantum
(A), keadaan kuantum  setelah dilakukan rotasi 180
setelah dilakukan rotasi 180 terhadap sumbu
terhadap sumbu  dengan menggunakan gerbang Pauli-X , dan keadaan superposisi antara
dengan menggunakan gerbang Pauli-X , dan keadaan superposisi antara  dan
dan  dengan gerbang Hadamard (C).
dengan gerbang Hadamard (C).
Gerbang Hadamard
Gerbang Hadamard berfungsi untuk mengubah keadaan qubit menjadi superposisi dari  dan
dan  . Dalam bentuk matriks, gerbang Hadamard dituliskan sebagai:
. Dalam bentuk matriks, gerbang Hadamard dituliskan sebagai:
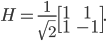
Jika kita terapkan pada qubit  akan menghasilkan
akan menghasilkan

Sedangkan jika kita terapkan pada qubit  akan diperoleh
akan diperoleh

Dalam bola Bloch, gerbang Hadamard merotasikan vektor sebesar 180 terhadap sumbu diagonal antara sumbu-
terhadap sumbu diagonal antara sumbu- dan sumbu-
dan sumbu- (Gambar 2C).
(Gambar 2C).
Gerbang CNOT (controlled NOT)
Gerbang CNOT bekerja layaknya gerbang XOR (exclusive OR) di komputasi klasik. Gerbang XOR mengubah bit pada masukan kedua (B) jika dan hanya jika masukan pertama (A) adalah 1, perhatikan tabel berikut:
| A | B | A XOR B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Gerbang CNOT bekerja pada dua qubit, dengan qubit pertama berfungsi sebagai pengendali (control) sedang qubit kedua sebagai target yang akan diubah keadaannya. Sama halnya dengan gerbang XOR, qubit target akan berubah keadaanya jika dan hanya jika qubit pengendali adalah  .
.

Gambar 3. Gerbang CNOT mengubah keadaan kuantum qubit kedua jika masukan qubit pertama (kontrol) adalah  .
.
Pengukuran dalam komputasi kuantum
Pengukuran adalah proses yang penting dalam komputasi kuantum. Bagaimana kita melakukan pengukuran menentukan kredibilitas hasil akhir dari komputasi kuantum. Dalam komputasi kuantum pengukuran harus dilakukan di akhir proses komputasi. Jika tidak, sifat kuantum yang menjadi pembeda dan keunggulan komputer kuantum dibanding komputer klasik akan musnah.
Dalam komputasi kuantum hanya proses perhitungan saja yang dilakukan secara kuantum, sedangkan hasil perhitungan akan menghasilkan bit klasik yang tentu dapat dipahami dan diinterpretasikan dalam berbagai bentuk seperti angka dan gambar oleh komputer klasik. Pengukuran akan memproyeksikan hasil perhitungan kuantum ke bit klasik berisi angka  atau
atau  . Karena itu, sekali pengukuran dilakukan terhadap hasil perhitungan kuantum, kita tidak akan bisa lagi melakukan komputasi kuantuam karena qubit telah berubah menjadi hanya bit.
. Karena itu, sekali pengukuran dilakukan terhadap hasil perhitungan kuantum, kita tidak akan bisa lagi melakukan komputasi kuantuam karena qubit telah berubah menjadi hanya bit.
Pengukuran dalam komputasi kuantum berarti probabilitas untuk menemukan qubit tertentu dan direpresentasikan dalam:

Simbol  yang mengapit
yang mengapit  di sebelah kanan tanda sama dengan disebut dengan bra, yang tidak lain adalah konjugat dari ket. Bra mengubah bentuk vektor ket yang semula vertikal menjadi vektor horizontal serta mengubah tanda jika vektor berupa bilangan kompleks (disimbolkan dengan
di sebelah kanan tanda sama dengan disebut dengan bra, yang tidak lain adalah konjugat dari ket. Bra mengubah bentuk vektor ket yang semula vertikal menjadi vektor horizontal serta mengubah tanda jika vektor berupa bilangan kompleks (disimbolkan dengan  ):
):

Sebagai contoh, jika kita punya keadaan kuantum superposisi  . Probabilitas ditemukannya qubit
. Probabilitas ditemukannya qubit  adalah:
adalah:

Hasil yang sama kan diperoleh jika kita menghitung probabilitas qubit  . Artinya, pada keadaan superposisi kita memiliki masing-masing 50% kemungkinan untuk menemukan qubit
. Artinya, pada keadaan superposisi kita memiliki masing-masing 50% kemungkinan untuk menemukan qubit dan
dan  . Hasil akhir pengukuran kuantum Dalam rangkaian kuantum, pengukuran disimbolkan oleh alat ukur dengan jarum penunjuk (Gambar 4).
. Hasil akhir pengukuran kuantum Dalam rangkaian kuantum, pengukuran disimbolkan oleh alat ukur dengan jarum penunjuk (Gambar 4).

Gambar 4. Gerbang pengukuran memproyeksikan hasil perhitungan kuantum  ke bit klasik
ke bit klasik  . Garis tunggal menggambarkan jalur kuantum, sedangkan garis ganda menggambarkan jalur klasik.
. Garis tunggal menggambarkan jalur kuantum, sedangkan garis ganda menggambarkan jalur klasik.
Menginstal Qiskit
Setelah mempelajari dasar komputasi kuantum, saatnya kita beralih pada pemrograman kuantum dengan Qiskit. Qiskit berjalan dengan menggunakan bahasa pemrograman python. Oleh karena itu hal pertama yang harus kita lakukan adalah menginstal python di komputer pribadi kita. Artikel sebelumnya telah membahas bagaimana menginstal python di komputer pribadi kita. Jadi anda tinggal mengkuti petunjuk yang diberikan di artikel tersebut.
Alternatif lain anda dapat menginstal Anaconda. Anaconda merupakan paket lengkap perangkat lunak pemrograman python. Di dalamnya sudah termasuk IDE (integrated development environment), yang dapat digunakan untuk menulis dan menjalankan kode-kode python, modul-modul, dan fungsi-fungsi yang berguna dalam pemrograman python. Anaconda dapat diunduh dan diinstal dengan mudah di komputer pribadi anda.
Dalam tutorial ini kita menggunakan Jupyter Notebook, sebuah perangkat lunak berbasis web yang dapat digunakan untuk membuat catatan berisi tulisan dan kode program yang dapat dijalankan secara langsung.
Qiskit bekerja di sistem 64-bit. Sistem operasi yang telah teruji dapat menjalankan qiskit adalah:
- Ubuntu 16.04 atau setelahnya
- Mac OS 10.12.6 atau setelahnya
- Windows 7 atau setelahnya
Setelah menginstal python dan pip, Qiskit dapat dengan mudah diinstal dengan mengetikkan perintah berikut di terminal (jika anda menggunakan sistem operasi Linux atau Mac):
pip install qiskit
Pemrograman qiskit akan lebih menarik dan mudah dimengerti jika kita menggunakan grafik untuk memvisualisasikan data, rangkaian kuantum, atau bola Bloch. Untuk menggunakan qiskit dengan visualisasi cukup ketikkan perintah berikut di terminal:
pip install qiskit[visualization]
Setelah sukses menginstal qiskit kita dapat coba menjalankan qiskit di Jupyter Notebook. Untuk memastikan, kita akan mengecek apakah qiskit benar terinstal di komputer pribadi kita dengan mengimpor modul qiskit kemudian mengecek versinya:
Out[2] berisi versi dari Qiskit yaang terinstal beserta elemen-elemen penyusunnya seperti terra, aer, ignis, dan aqua. Elemen-elemen ini dibutuhkan dalam pemrograman komputasi kuantum, antara lain untuk membuat rangkaian logika kuantum (terra), menyimulasikan komputasi kuantum (aer), mengatasi bising dan eror (ignis), dan membangun aplikasi nyata dari algoritma kuantum (aqua). Setelah ini anda sudah siap untuk membuat program kuantum pertama anda!
Referensi
- A. Asfaw, et al., Learn Quantum Computation Using Qiskit (The Jupyter Book Community, 2019). Diakses: 29 Agustus 2020. [Daring]. Tersedia di: http://community.qiskit.org/textbook.
- C. Bernhardt, Quantum Computing for Everyone. Cambridge, MA: The MIT Press, 2019.




Keren, mudah dipahami.